Understanding Young’s Modulus in Engineering and Material Science

In this article, we will explore the concept of Young’s modulus, an essential property in the field of engineering and material science. Young’s modulus, also known as the modulus of elasticity, plays a crucial role in understanding the behavior of materials under mechanical stress. We will delve into its definition, calculation, importance, and various applications across different material types.

In the following text, you will find a summary of the topics that will be addressed in this article.

Definition and Explanation of Young’s Modulus

Young’s modulus refers to the measure of the stiffness or rigidity of a material. It quantifies the material’s ability to deform under the influence of an applied force and return to its original shape once the force is removed. Young’s modulus is defined as the ratio of stress to strain within the elastic limit of a material. This modulus helps engineers predict how materials will respond to external forces and determine their suitability for specific applications.

Importance of Young’s Modulus

Young’s modulus is of utmost importance in engineering and material science. It provides valuable insights into the mechanical behavior and performance of materials. By understanding Young’s modulus, engineers can assess a material’s ability to withstand stress and deformation, making it possible to design safe and efficient structures. Additionally, Young’s modulus helps in material selection, ensuring that the chosen material meets the required mechanical properties for a given application.

Calculation of Young’s Modulus

The Young’s modulus of a material can be calculated using various methods, depending on the type of material and the available testing equipment. The most common approach involves subjecting a material to tensile or compressive forces and measuring the resulting strain. By dividing the stress (force per unit area) by the strain (deformation per unit length), Young’s modulus can be determined.

Young’s Modulus Formula (tensile test)

The most commonly used formula for calculating the modulus of elasticity in a tensile test is as follows:

Modulus of Elasticity (E) = Stress (σ) / Strain (ε), illustrated below.

In this formula, stress is the load applied to the specimen divided by the original cross-sectional area, and strain is the change in specimen length divided by the original length.

This formula allows determining the modulus of elasticity for the material in question, considering the elastic response during the tensile test.

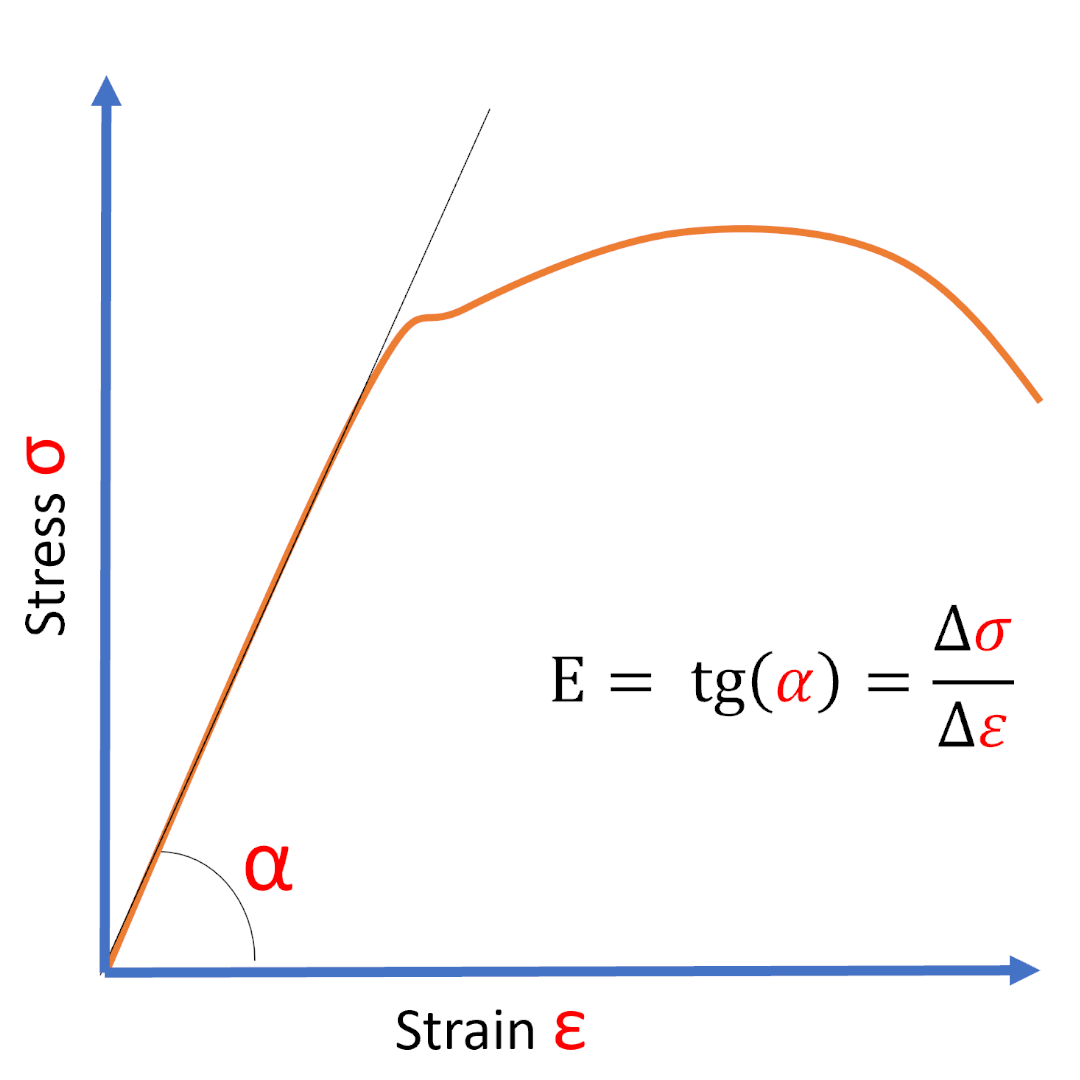
E =  Δσ /Δε 

Like this:

E = Modulus of elasticity or Young’s Modulus

σ = Stress

ɛ = Strain

Advantages of Using Young’s Modulus

Utilizing Young’s modulus offers several advantages in engineering and material science. Firstly, it enables engineers to compare and evaluate the mechanical properties of different materials objectively. This aids in material selection for specific applications, ensuring optimal performance. Secondly, Young’s modulus helps in the design and analysis of structures, predicting how materials will behave under various loading conditions. Lastly, this modulus facilitates the optimization of material usage, leading to cost-effective and sustainable engineering solutions.

Properties Obtained by Young’s Modulus

Young’s modulus provides valuable information about several properties of materials. By knowing the modulus, engineers can assess a material’s stiffness, flexibility, and resistance to deformation. It helps determine the material’s ability to withstand applied forces, its elastic limits, and its response to different types of stress. Young’s modulus also allows for the prediction of a material’s behavior in terms of compression, tension, and bending, which is essential for designing structures and components.

Metallic Materials

In metallic materials, Young’s modulus varies depending on factors such as crystal structure, temperature, and alloy composition. For instance, steel typically has a high Young’s modulus, providing excellent stiffness and strength. Other metals like aluminum and copper also exhibit significant moduli, making them suitable for various structural applications. Understanding the Young’s modulus of metallic materials is crucial for designing load-bearing components and ensuring their integrity.

Polymer Materials

Polymer materials generally possess lower Young’s moduli compared to metals. The Young’s modulus of polymers depends on factors such as molecular structure, cross-linking, and degree of crystallinity. Polymers like polyethylene and polypropylene exhibit relatively low moduli, making them flexible and suitable for applications requiring impact resistance. In contrast, thermosetting polymers, such as epoxy resins, can have higher moduli, providing rigidity and strength.

Ceramic Materials

Ceramic materials exhibit a wide range of Young’s moduli due to variations in composition, porosity, and crystal structure. Ceramic materials with dense and crystalline structures, like alumina and zirconia, tend to have high Young’s moduli, making them stiff and brittle. Porous ceramics, on the other hand, can have lower moduli, imparting improved toughness. Understanding the Young’s modulus of ceramic materials is essential for designing ceramic components and predicting their mechanical behavior.

Composite Materials

Composite materials, consisting of a combination of different constituents, possess unique mechanical properties influenced by the types and arrangements of their components. The Young’s modulus of composites can vary widely, depending on the proportion and orientation of reinforcing fibers or particles within the matrix material. Fiber-reinforced composites, such as carbon fiber reinforced polymers, exhibit high Young’s moduli, providing exceptional strength and stiffness while maintaining low weight.

Obtaining Young’s Modulus Data

To obtain Young’s modulus data for a specific material, various testing methods are employed. Tensile testing is commonly used for metals and polymers, where the material is subjected to tensile forces until failure while measuring the resulting strain. For ceramic materials, flexural testing is often employed, involving bending the material and measuring the strain. The obtained stress-strain data allows for the calculation of Young’s modulus.

Equipment for Determining Young’s Modulus

Several testing equipment and instruments are utilized to determine Young’s modulus accurately. Universal testing machines (UTMs) equipped with appropriate grips and fixtures are commonly employed for tensile testing of metallic and polymeric materials. In the case of ceramic materials, flexural testing machines, such as three-point or four-point bending setups, are used. These machines apply precise loads and measure the corresponding displacements required for calculating Young’s modulus.

Specimen for Young’s Modulus Testing

The choice of specimen for Young’s modulus testing depends on the material type and the desired testing method. For tensile testing, metallic and polymeric materials often employ dogbone-shaped specimens, while ceramic materials utilize rectangular bars for flexural testing. The dimensions of these specimens adhere to specific standards to ensure accurate and consistent results. Careful sample preparation and handling are crucial to obtain reliable Young’s modulus values.

Standards for Obtaining Young’s Modulus

Obtaining Young’s modulus data follows specific standards set by organizations like the International Organization for Standardization (ISO) and the American Society for Testing and Materials (ASTM). The main standards include:

• ISO 527: This standard provides guidelines for testing plastics, including methods for determining Young’s modulus under tensile stress.
• ISO 178: It provides guidelines for testing rigid plastics and composites using flexural methods to determine their flexural modulus, which is related to Young’s modulus.
• ISO 6721: It addresses the determination of Young’s modulus of solid materials by dynamic mechanical analysis (DMA), which measures the viscoelastic properties of materials.
• ASTM E8: It outlines procedures for testing metallic materials, specifically tensile testing, to determine Young’s modulus and other mechanical properties.
• ASTM C1161: This standard focuses on determining Young’s modulus in ceramic materials through flexural testing, which involves bending the material and measuring the resulting strain.
• ASTM D638: It specifies the testing method for determining Young’s modulus of plastics using a tensile testing machine.
• ASTM D790: This standard covers flexural testing of plastics and composites to determine their Young’s modulus and flexural strength.
• ASTM C469: This standard pertains to testing the flexural properties of concrete using a centrally loaded beam to determine Young’s modulus.

These standards ensure consistent testing procedures, specimen preparation, and calculation methods, allowing for accurate and reliable determination of Young’s modulus across different material types.

Examples of Materials and Young’s Modulus

• Steel (E = 200 GPa): With a high Young’s modulus, steel is widely used in construction, automotive, and aerospace industries due to its excellent strength and stiffness.
• Aluminum (E = 70 GPa): Aluminum exhibits a relatively high Young’s modulus while being lightweight, making it suitable for applications requiring a balance of strength and weight, such as aircraft structures.
• Polyethylene (E = 1-2 GPa): Polyethylene has a low Young’s modulus, providing flexibility and impact resistance. It finds applications in packaging, plastic bags, and various consumer products.
• Glass (E = 70-90 GPa): Glass possesses a high Young’s modulus, making it brittle but rigid. It is commonly used in windows, lenses, and fiber optics due to its transparency and optical properties.

Applications of Young’s Modulus

• Structural Engineering: Young’s modulus helps engineers design and analyze buildings, bridges, and other structures by predicting how materials will respond to loads and deformations.
• Material Selection: Young’s modulus aids in selecting suitable materials for specific applications based on their mechanical properties, ensuring optimal performance and durability.
• Manufacturing Processes: Understanding Young’s modulus helps in determining the feasibility and integrity of manufacturing processes such as injection molding, extrusion, and metal forming.
• Product Design: Young’s modulus plays a vital role in designing consumer products, automotive components, and medical devices, ensuring that they meet the required performance criteria.

Additional Information

Young’s modulus is temperature-dependent, and certain materials may exhibit changes in their modulus with varying temperatures. It is essential to consider this factor when designing structures or selecting materials for applications where temperature variations are significant. Additionally, Young’s modulus is an intrinsic material property and can provide insights into the material’s elasticity, but it does not account for factors like damping, creep, or fatigue, which may affect the material’s behavior under prolonged use.

Conclusion

Young’s modulus is a fundamental property in engineering and material science that allows for the understanding of material behavior under stress. By comprehending Young’s modulus, engineers can make informed decisions regarding material selection, design structures with the desired mechanical properties, and ensure the reliability and safety of various applications. Understanding the different moduli exhibited by different material types, including metals, polymers, ceramics, and composites, is crucial for their successful utilization in diverse industries.

FAQ

What is meant by Young’s modulus?

Young’s modulus, also known as the modulus of elasticity, is a measure of the stiffness or rigidity of a material. It quantifies the material’s ability to deform under an applied force and return to its original shape when the force is removed.

What is Young’s modulus in IB Physics?

In IB (International Baccalaureate) Physics, Young’s modulus is studied as a material property related to its elasticity. It is used to understand how materials respond to external forces and their ability to withstand stress and deformation.

What does a higher Young’s modulus mean?

A higher Young’s modulus indicates a stiffer material. It means that the material requires more force to produce a given amount of deformation or strain. Materials with higher Young’s modulus are generally more rigid and less prone to deformation under applied loads.

What is a simple example of Young’s modulus?

A simple example of Young’s modulus is a metal wire or spring. When a tensile force is applied to the wire or spring, it elongates or stretches. The relationship between the applied force and the resulting deformation provides information about the wire’s or spring’s Young’s modulus.

What is the difference between modulus and Young’s modulus?

Modulus is a general term that refers to a material’s measure of elasticity, including different types of elastic moduli. Young’s modulus is a specific type of modulus that specifically measures the stiffness or rigidity of a material within its elastic limit.

How do you use Young’s modulus?

Young’s modulus is used in engineering and materials science to understand and predict the behavior of materials under different loading conditions. It helps in material selection, structural design, and determining the mechanical properties of materials.

Is Young’s modulus the same as stiffness?

Yes, Young’s modulus is a measure of stiffness. It quantifies the resistance of a material to deformation when subjected to an applied force. A higher Young’s modulus corresponds to a stiffer material.

Is Young’s modulus the same as tensile strength?

No, Young’s modulus and tensile strength are not the same. Young’s modulus measures the stiffness or rigidity of a material, while tensile strength measures the maximum stress a material can withstand before it fails under tension.

What is the difference between Young’s modulus and tensile strength?

Young’s modulus describes the elastic response of a material to an applied force, while tensile strength represents the maximum stress a material can endure before breaking under tension. Young’s modulus focuses on deformation and elasticity, while tensile strength relates to the material’s ultimate failure under tension.

Does a higher Young’s modulus mean a stronger material?

A higher Young’s modulus does not necessarily mean a stronger material. Young’s modulus measures stiffness, while strength refers to a material’s ability to resist deformation or failure under applied loads.

Does a higher Young’s modulus mean stronger?

No, a higher Young’s modulus does not directly imply that a material is stronger. Young’s modulus measures stiffness, while strength refers to the material’s ability to resist deformation or failure under applied loads. Strength is influenced by various factors beyond Young’s modulus, such as the material’s microstructure, defects, and fracture toughness.

What material has the highest Young’s modulus?

Among common materials, diamond has the highest Young’s modulus. It possesses an exceptionally high stiffness due to its strong covalent bonds and highly ordered crystal lattice structure. Diamond has a Young’s modulus of approximately 1,200-1,300 GigaPascals (GPa).